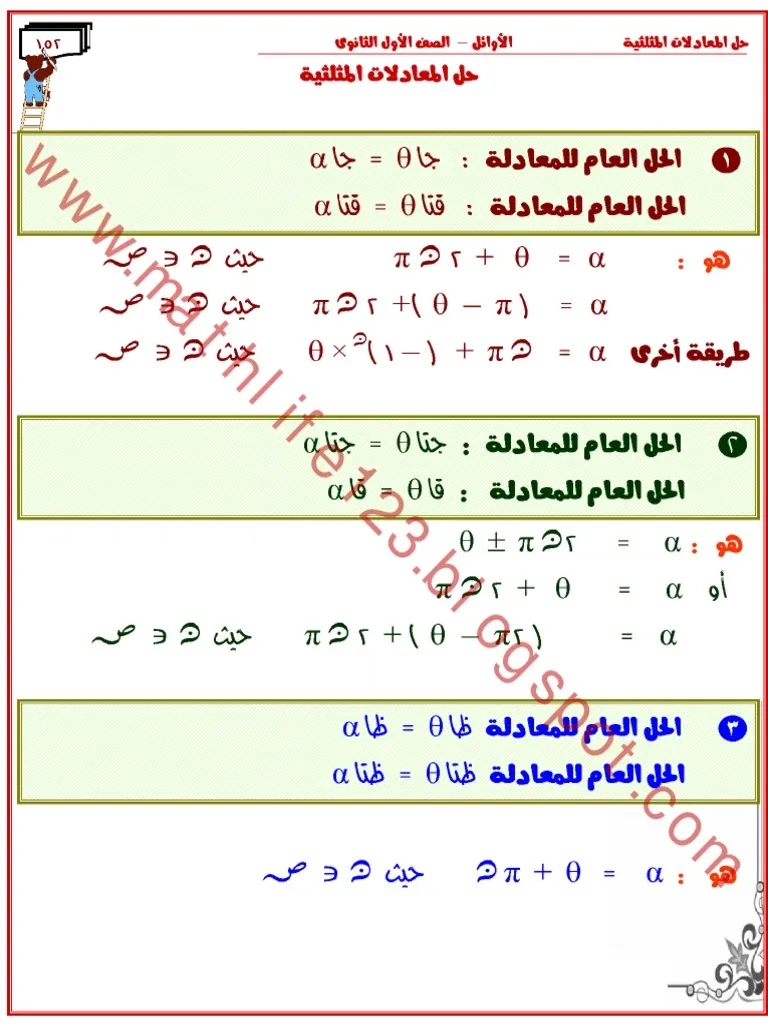
مراجعة حساب مثلثات أولي ثانوي ترم ثاني - حل المعادلات المثلثية
مستر / لطفي زهران
شاهد ايضا:
ما هي المعادلات المثلثية Trigonometric equations
إحدى أنواع المعادلات الرياضية، تتضمن الدوال المثلثية (Trigonometric Function) وهي Sin وCos وTan، والتي يمكن التحويل بينها لحل المعادلة والوصول إلى قيمة الزاوية المجهولة فيها.
بعض المعادلات المثلثية صحيحةٌ لأي زاويةٍ وتُدعى بالمتطابقة المثلثية (Trigonometric identity)، بينما تنطبق بعض المعادلات على زوايا محددة فقط وتُدعى بالمعادلات الشرطية (Conditional equation).
يمكن حل المعادلات المثلثية ضمن مجالٍ محددٍ يدعى بالحلول الأولية (Primary Solutions)، بينما يكون الحل العام عبارةً عن صيغةٍ تقدّم كافة الحلول الممكنة، ومن المهم معرفة أن الحل لا يعتمد على طرقٍ محددةٍ وخطواتٍ ثابتة؛ حيث تتطلب كل معادلةٍ طريقة حلٍ تختلف عن غيرها، وذلك باستخدام المتطابقات وأساليب الحل الجبرية. 1
حل المعادلات المثلثية
كما في المعادلات كثيرة الحدود والمعادلات النسبية، سنصل في نهاية الحل إلى قيمٍ محددةٍ للمتغير فقط، وتُعتبر هي الحل، فعادةً ما تُحل المعادلات المثلثية ضمن مجالٍ محددٍ.
لكن غالبًا ما سيُطلب عند حل المعادلة الوصول إلى كافة الحلول الممكنة، ولأن المتطابقات المثلثية دورية ستتكرر الحلول الناتجة خلال كل مجالٍ؛ بمعنى آخر قد نصل إلى عددٍ غير محدودٍ من الحلول للمعادلات المثلثية، ولذلك يجب تحديد مجال العمل قبل اعتماد أحد الحلول.
لا يختلف حل المعادلات المثلثية عن المعادلات الجبرية، حيث تُقرأ المعادلة من اليسار إلى اليمين بشكلٍ أفقيٍّ، ثم يُبحث في البداية عن النماذج الشائعة والعوامل المشتركة، ثم تُستبدل بعض الصيغ التي تتضمن قيمًا مجهولةً، ليُصبح حل المعادلة بشكلٍ أبسط وبطريقةٍ مباشرة، كما يُمكن الاعتماد على المتطابقات المثلثية في إيجاد الحل.2
مبدأ حل المعادلات المثلثية
يعتمد حل المعادلات المثلثية على تحويلها إلى إحدى المعادلات المثلثية الأساسية الأربعة وهي Sin(x)=a وCos(x)=a وTan(x)=a وcot(x)=a، والتي يعتمد حلها على دراسة مواقع القوس x في الدائرة المثلثية، واستخدام جدول التحويلات المثلثية أو الآلة الحاسبة.
ولتحويل المعادلة إلى معادلةٍ مثلثيةٍ أساسية يجب الاعتماد على التحويلات الجبرية، وخصائص الدوال المثلثية، والمتطابقات المثلثية، إضافةً للمتطابقات التحويلية.
يجب قبل البدء بحل المعادلة المثلثية إيجاد الأقواس المعروفة بحسب المتطابقات المثلثية، والحصول على قيم تحويل الأقواس من خلال الجداول المثلثية أو الآلة الحاسبة، فمثلًا عند حل المعادلة Cos(x)=0.732 ستُعطي الآلة الحاسبة درجة القوس arc(x)=42.95، بينما من خلال دائرة الوحدة المثلثية سنحصل على كافة الأقواس بنفس قيمة الـ cos.
إحدى أنواع المعادلات الرياضية، تتضمن الدوال المثلثية (Trigonometric Function) وهي Sin وCos وTan، والتي يمكن التحويل بينها لحل المعادلة والوصول إلى قيمة الزاوية المجهولة فيها.
بعض المعادلات المثلثية صحيحةٌ لأي زاويةٍ وتُدعى بالمتطابقة المثلثية (Trigonometric identity)، بينما تنطبق بعض المعادلات على زوايا محددة فقط وتُدعى بالمعادلات الشرطية (Conditional equation).
يمكن حل المعادلات المثلثية ضمن مجالٍ محددٍ يدعى بالحلول الأولية (Primary Solutions)، بينما يكون الحل العام عبارةً عن صيغةٍ تقدّم كافة الحلول الممكنة، ومن المهم معرفة أن الحل لا يعتمد على طرقٍ محددةٍ وخطواتٍ ثابتة؛ حيث تتطلب كل معادلةٍ طريقة حلٍ تختلف عن غيرها، وذلك باستخدام المتطابقات وأساليب الحل الجبرية. 1
حل المعادلات المثلثية
كما في المعادلات كثيرة الحدود والمعادلات النسبية، سنصل في نهاية الحل إلى قيمٍ محددةٍ للمتغير فقط، وتُعتبر هي الحل، فعادةً ما تُحل المعادلات المثلثية ضمن مجالٍ محددٍ.
لكن غالبًا ما سيُطلب عند حل المعادلة الوصول إلى كافة الحلول الممكنة، ولأن المتطابقات المثلثية دورية ستتكرر الحلول الناتجة خلال كل مجالٍ؛ بمعنى آخر قد نصل إلى عددٍ غير محدودٍ من الحلول للمعادلات المثلثية، ولذلك يجب تحديد مجال العمل قبل اعتماد أحد الحلول.
لا يختلف حل المعادلات المثلثية عن المعادلات الجبرية، حيث تُقرأ المعادلة من اليسار إلى اليمين بشكلٍ أفقيٍّ، ثم يُبحث في البداية عن النماذج الشائعة والعوامل المشتركة، ثم تُستبدل بعض الصيغ التي تتضمن قيمًا مجهولةً، ليُصبح حل المعادلة بشكلٍ أبسط وبطريقةٍ مباشرة، كما يُمكن الاعتماد على المتطابقات المثلثية في إيجاد الحل.2
مبدأ حل المعادلات المثلثية
يعتمد حل المعادلات المثلثية على تحويلها إلى إحدى المعادلات المثلثية الأساسية الأربعة وهي Sin(x)=a وCos(x)=a وTan(x)=a وcot(x)=a، والتي يعتمد حلها على دراسة مواقع القوس x في الدائرة المثلثية، واستخدام جدول التحويلات المثلثية أو الآلة الحاسبة.
ولتحويل المعادلة إلى معادلةٍ مثلثيةٍ أساسية يجب الاعتماد على التحويلات الجبرية، وخصائص الدوال المثلثية، والمتطابقات المثلثية، إضافةً للمتطابقات التحويلية.
يجب قبل البدء بحل المعادلة المثلثية إيجاد الأقواس المعروفة بحسب المتطابقات المثلثية، والحصول على قيم تحويل الأقواس من خلال الجداول المثلثية أو الآلة الحاسبة، فمثلًا عند حل المعادلة Cos(x)=0.732 ستُعطي الآلة الحاسبة درجة القوس arc(x)=42.95، بينما من خلال دائرة الوحدة المثلثية سنحصل على كافة الأقواس بنفس قيمة الـ cos.